- By Rowan Lea
- ·
- Posted Jan 25, 2024 10:21:11 AM
Songbird
Inspired by the creative works of Gawain Hewitt: https://gawainhewitt.co.uk/
Sudoku is a very popular number-placement puzzle.
The objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 regions that compose the grid contain all of the digits from 1 to 9.
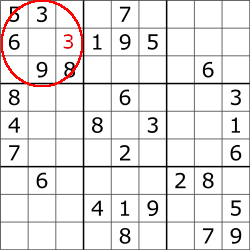
The starting point is a partially completed grid:
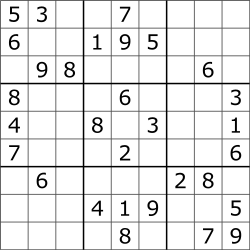
The final one would like this:

The following are examples of violations:
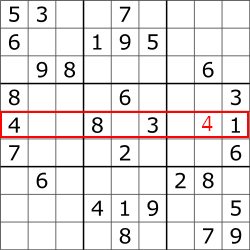
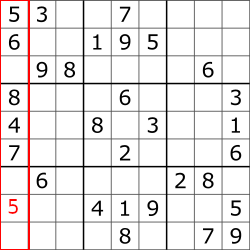
Neither one of these can be present in a valid solution.
This kata is divided into four levels of increasing difficulty. Start with the first and work your way up.
Note: This level is meant to get you familiar with the rules of the game. If you already know them well (for instance, if you practice Sudoku in real life), you can safely skip it and go straight into Level 1.
Create an application capable of determining whether a matrix is a potential solution for a Sudoku.
The input is the path a CSV file containing N rows and N numbers per row, where N is the square of an integer greater than 3 (4, 9, 16, 25,...).
The file contents form a matrix, which you need to check for rules violations.
Example:
Given a file containing:
1,2,3,4,
2,1,4,3,
3,4,1,2,
4,3,2,1,
The output should be:
The input doesn't comply with Sudoku's rules.
Given a file containing:
1,2,3,4,
3,4,1,2,
2,3,4,1,
4,1,2,3,
The output should be:
The input complies with Sudoku's rules.
Create an application capable of determining whether a proposed solution is valid for a given initial grid.
The input is the path to two CSV files containing N rows and N numbers per row, where N is the square of an integer greater than 3 (4, 9, 16, 25,...).
Example:
5,3, , ,7, , , , ,
6, , ,1,9,5, , , ,
,9,8, , , , ,6, ,
8, , , ,6, , , ,3,
4, , ,8,7,3, , ,1,
7, , , ,2, , , ,6,
,6, , , , ,2,8, ,
, , ,4,1,9, , ,5,
,1, , ,8, , ,7,9,
The following are a few examples of incorrect solutions proposed (contents of the second input file):
| 5,3, , ,7, , , , , 6, , ,1,9,5, , , , ,9,8, , , , ,6, , 8, , , ,6, , , ,3, 4, , ,8,7,3, , ,1, 7, , , ,2, , , ,6, ,6, , , , ,2,8, , , , ,4,1,9, , ,5, ,1, , ,8, , ,7,9, |
5,3,4,5,7,8,9,1,2, |
4,5,3,8,2,6,1,9,7, 8,9,2,5,7,1,6,3,4, 1,6,7,4,9,3,5,2,8, 7,1,4,9,5,2,8,6,3, 5,8,6,1,3,7,2,4,9, 3,2,9,6,8,4,7,5,1, 9,3,5,2,1,8,4,7,6, 6,7,1,3,4,5,9,8,2, 2,4,8,7,6,9,3,1,5, |
In any of these cases the output should be
The proposed solution is incorrect
This is an example of a correct solution
5,3,4,6,7,8,9,1,2,
6,7,2,1,9,5,3,4,8,
1,9,8,3,4,2,5,6,7,
8,5,9,7,6,1,4,2,3,
4,2,6,8,5,3,7,9,1,
7,1,3,9,2,4,8,5,6,
9,6,1,5,3,7,2,8,4,
2,8,7,4,1,9,6,3,5,
3,4,5,2,8,6,1,7,9,
In this case, the output should be
The proposed solution is correct
Hint: think about all the reasons why a proposed solution might be wrong. If none of them is true for the specific instance you're checking, then it must be accepted.
Create an application to provide a valid solution given the initial grid or a message in case the Sudoku is not solvable.
The input is CSV file with the same format as in the first level and the output is a CSV string containing the solution found in case it exists.
Example:
For an input like
5,3, , ,7, , , , ,
6, , ,1,9,5, , , ,
,9,8, , , , ,6, ,
8, , , ,6, , , ,3,
4, , ,8, ,3, , ,1,
7, , , ,2, , , ,6,
,6, , , , ,2,8, ,
, , ,4,1,9, , ,5,
, , , ,8, , ,7,9,
The output should be
5,3,4,6,7,8,9,1,2,
6,7,2,1,9,5,3,4,8,
1,9,8,3,4,2,5,6,7,
8,5,9,7,6,1,4,2,3,
4,2,6,8,5,3,7,9,1,
7,1,3,9,2,4,8,5,6,
9,6,1,5,3,7,2,8,4,
2,8,7,4,1,9,6,3,5,
3,4,5,2,8,6,1,7,9,
And for an input like
5,3, , ,7, , , , ,
6, , ,1,9,5, , , ,
,9,8, , , , ,6, ,
8, , , ,6, , , ,3,
4, , ,8, ,3, , ,1,
7, , , ,2, , , ,6,
6, , , , , ,2,8, ,
, , ,4,1,9, , ,5,
, , , ,8, , ,7,9,
The output should be
The Sudoku is not solvable
Hints:
1, ,3,4,
3,4,1,2,
,3,2,1,
4,1, ,3,
Create an application which can produce a solvable NxN initial grid.
In this case the input is the grid dimension and the initial number of blank spaces.
The output is a CSV string with the format discussed in the previous cases or a message stating that the requirements are not satisfiable.
Example:
For an input like:
3 51
The output should be something like:
5,3, , ,7, , , , ,
6, , ,1,9,5, , , ,
,9,8, , , , ,6, ,
8, , , ,6, , , ,3,
4, , ,8, ,3, , ,1,
7, , , ,2, , , ,6,
,6, , , , ,2,8, ,
, , ,4,1,9, , ,5,
, , , ,8, , ,7,9,
Hints:

Inspired by the creative works of Gawain Hewitt: https://gawainhewitt.co.uk/

What do we want to build? We are building a shopping cart for an online grocery shop. The idea of this kata is to build the product in an iterative..

Iteration 1 Business rules We want to build an ATM machine and the first thing we need to do, is to create the software that will breakdown which..
Join our newsletter for expert tips and inspirational case studies
Join our newsletter for expert tips and inspirational case studies